暨南大学通用机器学习团队取得突破性进展，提出解决经典韦伯区位问题奇异性难题的全新方法！该团队由网络空间安全学院和信息科学技术学院的教师、学生组成，研究方向涵盖通用逼近理论、分布外泛化、非凸优化等多个领域。自2024年4月至12月，团队已在icml（2篇）、neurips、ijcai、aaai等顶级人工智能会议上发表5篇论文，展现了强大的科研实力。本文第一作者为赖兆荣，通讯作者为李程博士。

韦伯区位问题的奇异性挑战

韦伯区位问题，源于费马点问题，广泛应用于机器学习、人工智能等多个领域。该问题旨在寻找一个中心点，最小化该点到多个给定点的加权距离之和。然而，该问题的求解过程容易遭遇奇异性问题，导致算法无法收敛。 这种奇异性可能出现在二维及更高维空间中，且难以通过简单的随机扰动等方法解决。

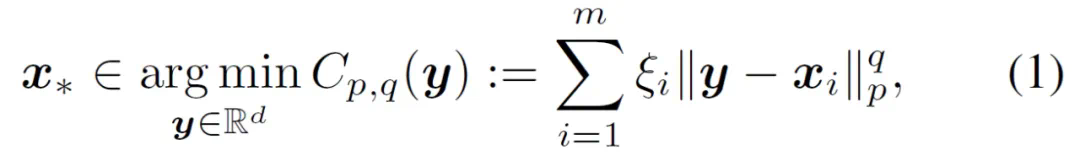
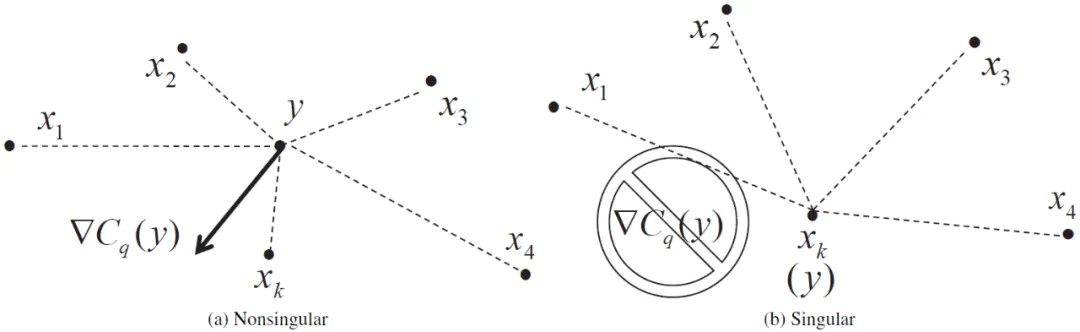
创新方案：去奇异性次梯度法

该团队提出了一种创新的“去奇异性次梯度法”，有效解决了这一难题。该方法通过识别并去除导致奇异性的数据点和维度，构建了“去奇异性次梯度”，并基于Weiszfeld算法，开发出一种名为qPpNWAWS的算法。

实验验证与应用

团队在CSI300数据集上进行了实验，结果表明qPpNWAWS算法具有高效性和高收敛速度。此外，在在线资产配置实验中，该算法也取得了优异的投资得分。

通用机器学习研究方向

该团队的研究属于通用机器学习领域的基础模块开发与优化器开发方向，致力于攻克通用人工智能中的基础科学与技术难题。

• 论文[a]：Invariant Risk Minimization Is A Total Variation Model (ICML 2024)
• 论文[b]：Autonomous Sparse Mean-CVaR Portfolio Optimization (ICML 2024)
• 论文[c]：A Globally Optimal Portfolio for m-Sparse Sharpe Ratio Maximization (NeurIPS 2024)
• 论文[d]：A De-singularity Subgradient Approach for the Extended Weber Location Problem (IJCAI 2024)

参考文献 (略，原文已列出)

• 论文标题：De-singularity Subgradient for the q-th-Powered L_p-Norm Weber Location Problem
• 论文链接：https://www.php.cn/link/5ecc4617cc84104f472db907a80372a0
• 项目地址：https://www.php.cn/link/2562b3fcf3a15d7926bde2ff91919d3d

感谢您的来访，获取更多精彩文章请收藏本站。